Die Geschwindigkeit von Erdsatelliten
Die Geschwindigkeit von Erdsatelliten
Ein Blick zum Himmel in einer sternklaren Nacht, gewährt uns nicht nur den gewohnten Anblick von Sternen, Sternhaufen, manchmal auch Planeten und sogar Sternschnuppen. Wenn man ein Fernglas zu Hilfe nimmt, kann man auch Galaxien erkennen. Zu bestimmten Zeitpunkten kann man auch schnell durch die Sternkonstellationen huschende, nicht blinkende, mehr oder weniger helle Lichtpunkte sehen. Das sind Satelliten, die um die Erde kreisen, und zur Übermittlung von Signalen von der Erde zur Erde benutzt werden. Auch die Internationale Raumstation, die in ihrem Endausbaustadium die Größe eines Fußballfeldes erreicht, kann man auf diese Weise wahrnehmen. Die genauen Zeitpunkte kann man unter Heaven’s above abrufen. In diesem Zusammenhang stellt sich die Frage nach der Geschwindigkeit dieser Objekte.
Die Ableitung dieser Geschwindigkeit mittels rein geometrischer Methoden, die von Newton und Feynman benutzt wurden, sollen hier vorgestellt werden, da sie nur Basiskenntnisse der Physik und Geometrie erfordern und somit von einem großen Kreis der Leser nachvollzogen werden können.
 Als Beispiel nehmen wir einen Schuß, der auf der Erdoberfläche in horizontaler Richtung abgegeben wird. Jedes Objekt, unabhängig von der Masse, fällt auf der Erde in der ersten Sekunde um 5m (genau um 9.81/2m). Dies gilt auch für horizontale Bewegungen, wie etwa eine abgeschossene Gewehrkugel. Gibt man der Gewehrkugel eine hohe horizontale Anfangsgeschwindigkeit, so bleibt es durch die Erdkrümmung im gleichen Abstand zur Erdoberfläche, und das Geschoss kann um die Erde herumfliegen. (Wir gehen von einer Vereinfachung ohne Berücksichtigung des Luftwiderstandes aus).
Als Beispiel nehmen wir einen Schuß, der auf der Erdoberfläche in horizontaler Richtung abgegeben wird. Jedes Objekt, unabhängig von der Masse, fällt auf der Erde in der ersten Sekunde um 5m (genau um 9.81/2m). Dies gilt auch für horizontale Bewegungen, wie etwa eine abgeschossene Gewehrkugel. Gibt man der Gewehrkugel eine hohe horizontale Anfangsgeschwindigkeit, so bleibt es durch die Erdkrümmung im gleichen Abstand zur Erdoberfläche, und das Geschoss kann um die Erde herumfliegen. (Wir gehen von einer Vereinfachung ohne Berücksichtigung des Luftwiderstandes aus).
Um eine kreisförmige Bahn um die Erde zu erreichen muss man also eine bestimmte Geschwindigkeit haben, die es jetzt zu ermitteln gilt. Auf der Skizze ist die Erde dargestellt. x ist die gesuchte Geschwindigkeit, y die Fallstrecke in einer Sekunde.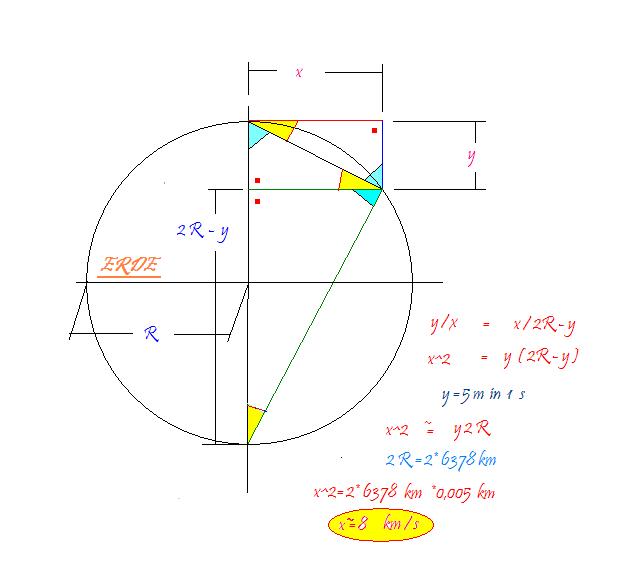
Die angeschrieben Gleichung ergibt sich durch geometrische Gesetze die seit Euklid bekannt sind und die Vereinfachung von x2=y(2R-y)=y2R-y2 zu x2=y2R ergibt sich daraus, dass y2 vernachlässigt werden kann.
Den Beweis für den aufgezeigten Zusammenhang überlasse ich dem Leser, da ich ihm das Vergnügen nicht nehmen will. Falls es jedoch zum Frust ausartet, sende mir eine E-Mail, lieber Leser, ich bin gerne behilflich.
Da der Erddurchmesser bekannt ist und damit die Erdkrümmung und die Fallstrecke eines Körpers auf der Erde in 1 Sekunde, ergibt sich durch das einsetzen der Werte eine Geschwindigkeit von knapp 8 km/s. Ist die Geschwindigkeit größer, wird die Bahn zur Ellipse.
 Die Internationale Raumstation (ISS) z.B. (siehe Skizze) fliegt in 358 km – 365 km Höhe und umrundet die Erde 15,69 mal pro Tag, also 1 mal in ca. 1,5 Stunden oder 90 Minuten. Durch die Flughöhe fliegt sie etwas langsamer, da man jetzt für R den Erdradius + Flughöhe in die Gleichung einsetzen muss, weiter ist durch die Höhe auch die Fallstrecke entsprechend der geringeren Gravitationskraft etwas geringer.
Die Internationale Raumstation (ISS) z.B. (siehe Skizze) fliegt in 358 km – 365 km Höhe und umrundet die Erde 15,69 mal pro Tag, also 1 mal in ca. 1,5 Stunden oder 90 Minuten. Durch die Flughöhe fliegt sie etwas langsamer, da man jetzt für R den Erdradius + Flughöhe in die Gleichung einsetzen muss, weiter ist durch die Höhe auch die Fallstrecke entsprechend der geringeren Gravitationskraft etwas geringer.
Zur Beobachtung von Satelliten gibt es noch den Beitrag “Beobachtung künstlicher Satelliten”
Willy Mahl, 20.06.2004
Letzte Änderung am 03.09.2004 durch astroman

Hinterlasse einen Kommentar
An der Diskussion beteiligen?Hinterlasse uns deinen Kommentar!