Die Dimensionen des Sonnensystems in 5 Schritten Gliederung 1. Erde2. Erdsatellit3. Mond4. Sonne5. Planetensystem
Die Dimensionen des Sonnensystems in 5 Schritten
Gliederung
Gliederung
1. Der Erdumfang
Im 5. Jahrhundert vor unserer Zeitrechnung hat Aristoteles bereits Autoren zitiert, die den Erdumfang mit 400 000 Stadien angegeben haben. Da wir das genaue Mass der Stadien, das sich wohl auch des öfteren geändert hat, nicht kennen, können wir auch nicht beurteilen, wie genau dieser Wert war. Die erste exakte Messung, die uns überliefert ist, stammt von Eratosthenes aus Cyene (276-195 v. Chr.). Die Messung soll eine gute Übereinstimmung mit der tatsächlichen Größe der Erde ergeben haben. Dies ist umso erstaunlicher, als die Messstrecke “A” durch Abschreiten ermittelt wurde, und die dazugehörige Winkelmessung auch nicht einfach war. 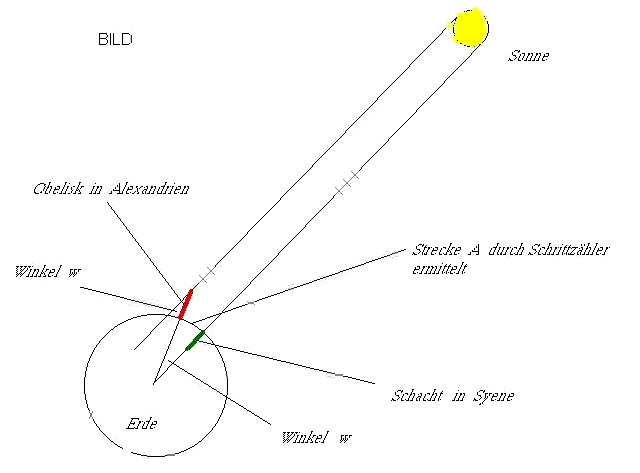
DieWinkelmessung am Obelisken musste zum gleichen Zeitpunkt vorgenommen werden, zu dem die Sonne senkrecht über dem Schacht stand.
Verwendete Größen
RRadius der ErdeU Umfang der Erde = 2*Pi*rwDer Schattenwinkel ist w = 7,5°, an einem Obelisken in Alexandrien gemessen.A Strecke zwischen einem Schacht in Syene (in den die Sonne zu einem bestimmten Zeitpunkt bis zum Grund vordringt, und damit senkrecht über dem Schacht steht) und dem Obelisken, an dem der Schattenwinkel abgelesen wird.
Dann ist : U / A = 360°/7,5°
Wenn also der Schattenwinkel und die Strecke A bekannt sind, lässt sich der Umfang der allerdings zur Kugel idealisierten Erde berechnen.
Aus U = 2*R*Pi lässt sich dann der Radius und damit der Erddurchmesser bestimmen.
2. Beobachten und Auswerten der Bahnen von Erdsatelliten
Einem Beobachter, der regelmässig den Sternenhimmel beobachtet, ist mit Sicherheit schon aufgefallen, dass es da gelegentlich Objekte gibt, die mit der Helligkeit eines hellen Sterns und oft noch heller, den Himmel von West nach Ost überqueren. 1 1/2 Stunden später passiert dasselbe noch einmal, aber an einer anderen Stelle des Himmels. Wir haben es hier mit einem erdgebundenen, künstlichen Satelliten zu tun, der in nahezu kreisförmigen Bahnen die Erde umrundet.
Wenn wir die Zeit ermitteln, in der er seine Bahn in Bezug zum Fixsternhimmel (siderische Umlaufperiode) vollendet, können wir ausrechnen, wie hoch sich der Satellit über der Erdoberfläche befindet.
Führt man nun folgende Größen ein
gErdbeschleunigung (bzw. “Ortsfaktor”) auf der Erdoberfläche,g’Erdbeschleunigung in der Satellitenbahn,R’Radius der Kreisförmigen Satellitenbahn,
und wendet man das sogenannte Gravitationsgesetz an, so läßt sich folgende Beziehung ableiten:g’ / g = (R/R’)2 => g’ = g (R / R’)2
Um das Gleichgewicht der Bahn zu gewährleisten, muss die Fliehkraft die Anziehungskraft, also die Gravitation aufheben (genaugenommen bringt die Gravitationskraft die Zentripetalkraft auf, damit der Körper auf der Kreisbahn bleibt). Die Fliehkraft in der kreisförmigen Bahn beträgt: g’ = v2 / R’
Damit erhalten wir: v2 / R’ = g (R / R’)2 (Gl. 1), wobei v die Bahngeschwindigkeit des Satelliten ist. Mit T als Umlaufzeit des Satelliten ergibt sich: v = (2 Pi R’) / T , eingesetzt in (Gl. 1) ergibt die Gleichung: 4 Pi2 * R’2 / T2 * R’ = g (R / R’)2, oder: R’3 = g * R2 * T2 / 4 * Pi2für R = 6 400 km = 6 400 000 mg = 9,81 m/s2T = 90m = 5 400s zum Beispiel erhält man für R’ = 6 670 000 m = 6 670 km, das sind 270 km über dem Erdradius R = 6 400 km.
Die Höhe des Satelliten über der Erdoberfläche ist also 270 km.
3. Die Entfernung des Mondes
Mit dem nächsten Schritt ermitteln wir mit den Keplerschen Gesetzen die Entfernung des Mondes, der ja ebenfalls ein Erdtrabant ist.
Dazu benötigen wir das 3. Keplersche Gesetz. Es lautet: T2 / R3 = const.
TUmlaufzeit in der Bahn (siderische, siehe oben)RBahnradiusconstEine Konstante, die abhängig vom Zentralkörper ist, in diesem Fall ist der Zentralkörper ja in beiden Fällen die Erde.
Wenn wir jetzt die Satellitendaten (RS, TS) und die wiederum siderische Umlaufzeit des Mondes (TM), die ja durch Beobachtung bekannt ist, in diese Gleichung einbringen, so erhalten wir:
(TM / TS)2 = ( RM / RS )3
Folgende Werte zum Einsetzten:TM = 27,32 Tage = 656 Stunden, siderische Umlaufzeit des Mondes.TS = 1 1/2h, Satellitenumlaufzeit, s.o.RS = 6 670 km, Radius der Satellitenbahn, s.o.
So ergibt sich für die Monddistanz RM = ((656 / 1,5)2)1/3 * 6 670 km = 384 297 km
Dies entspricht recht gut der mittleren Monddistanz. (zur Erinnerung, unsere Rechnung basiert auf einer angenommenen Kreisbahn!).
4. Das Gravitationsgesetz
Nachdem im Jahr 1798 die Gravitationskonstante ermittelt worden war, konnte man mit Hilfe des Gravitationsgesetzes auch die Masse der Erde bestimmen:
F = G * M * m / r2
Größen:
F = Anziehungskraft der Körper.G = 6,67*10-11, Gravitationskonstante.M = Masse des einen Körpers, hier die Erdmasse.m = Masse des anderen Körpers, hier die der umlaufende Masse, also des Satelliten.r = Bahnradius, hier Radius der Satellitenbahn.
Aus der Gleichsetzung der Gravitationskraft und Fliehkraft unseres Satelliten erhalten wir seine Zentralmasse , also die Erdmasse:
m v2 / r = G * M * m / r2 <=> M = r * v2 / G = 6*1024 kgNun haben wir die Masse der Erde mit der Hilfe eines die Erde umlaufenden Objektes
ermittelt. Durch die Bahndaten des Satelliten hat sich die Zentralmasse, in diesem Fall die Erdmasse, ergeben. Dieselbe Methode wenden wir jetzt an, um die Masse der Sonne zu ermitteln.
Allgemein kann man sagen, wenn man die Dimensionen des Sonnensystems ermitteln will, muss man seine Zentralmasse, also die Sonnenmasse kennen, und die Umlaufzeit der Planeten. Aus den Größen Zentral-Masse, Umlaufzeit, Bahnradius lässt sich eine Grösse errechnen, wenn die 2 übrigen bekannt sind.
Daher müssen wir jetzt, um die Sonnenmasse zu bestimmen, einen Planeten haben, dessen Umlaufzeit und Abstand von der Sonne bekannt ist. Als Prototyp bietet sich hierfür unsere Erde an, von der aus wir beobachten können. Um den Abstand der Erde von der Sonne zu ermitteln, benötigen wir Messmethoden auf der Basis der Geometrie. Das erfordert genaue Beobachtungsdaten, wenn man gute Ergebnisse bekommen möchte. Eine historische Methode ist das seltene Ereignis des Venusdurchgangs durch die Sonnenscheibe, das wir von der Erde aus beobachten können.
Wenn die Venus zwischen Sonne und Erde und zudem noch im, oder nahe des Bahnknotens steht (Die Venusbahn ist gegen die Erdbahn geneigt ), und dann von der Erde aus beobachtbar, über die Sonnenscheibe wandert, kann daraus der Beobachter auf 2 verschiedenen geographischen Breiten auf der Erde, aus den Ein- und Austrittszeiten der Venus vor der Sonnenscheibe den Winkelabstand bestimmen, der dem Abstand der Standorte auf der Erde entspricht. Aus dem 3. Keplergesetz kann man leicht die Abstände der Erde und Venus von der Sonne ableiten:
Es ist RV3/RE3 = ( TV/TE )2
RVRadius der Venusbahn um die Sonne.RERadius der Erdbahn um die Sonne.TVUmlaufzeit der Venus.TEUmlaufzeit der Erden.
Setzen wir nun RE=1, so erhalten wir den relativen Abstand der Venus von der Sonne im Vergleich zur Erde: RV/RE = ( TV/TE )2/3bzw. RV/RE = 0,723/1
Da der Abstand A (in km) der Beobachter auf der Erde bekannt ist und w als Winkelabstand (in Bogensekunden) der Bahnen der Venusscheibchen vor der Sonne durch Beobachtung ermittelt wurde, kann man die Sonnendistanz RE (in km), nach folgender Formel ermitteln: RE = 538 000 * A / w
Auf diese Weise wurde ein Wert von 151 225 000 km ermittelt, der genaue Wert ist 149 597 892 km = 1 AE
Die Ermittlung des Winkelabstandes und weitere Details werden in einem separaten Beitrag, siehe Venustransit, beschrieben.
5. Dimensionen des Planetensystems
Da wir den Erdabstand von der Sonne nun kennen, benutzen wir die bereits von der Ermittlung der Erdmasse (siehe oben) bekannte Gleichung: Fliehkraft = Gravitationskraft (bzw. : Zentripetalkraft = Gravitationskraft)
m * v2 / R = G * M * m / R2
mMasse des PlanetenvBahngeschwindigkeit des PlanetenRRadius der Planetenbahn um die SonneGGravitationskonstanteMSonnenmasse
Die Masse des Planeten kürzt sich heraus, sie spielt also keine Rolle bei der Bewegung um einen Zentralkörper mit sehr großer Masse und hat ihre Analogie in der Massenunabhängigkeit der Fallgeschwindigkeit eines Körpers auf der Erde
Mit v = 2 * Pi * R / T folgt aus obiger Gleichung R3 = G * M * T2 / 4 * Pi2, oder anders ausgedrückt: R3 / T2 = Konstant (3. Keplersches Gesetz )
Die Masse der Sonne ergibt sich dann zu: M = R3 * 4 * Pi2 / G * T2, wobei wir nun für R den mittleren Erdbahnradius und für T die siderische Umlaufzeit der Erde um die Sonne einsetzen. So erhalten wir M = 1,989*1033 g = 1,989 * 1030 kg
Wir sind jetzt in der Lage, den Abstand von jedem beliebigen Körper im Sonnensystem, der die Sonne als Zentralmasse umrundet und eine bekannte Umlaufzeit hat, zu bestimmen.
In der Astronomie wird der mittl. Abstand der Erde von der Sonne mit 1 AE (1 Astronomische Einheit) bezeichnet und sie beträgt knapp 150 Mio. km (siehe oben)
Wenn wir den Abstand Erde-Sonne RE = 1 setzen, ergibt sich für jeden beliebigen Planeten X ein mittlerer Abstand von: RX = ( TX/TE )2/3Das Ergebnis von RXist der mittlere Bahnradius des Planeten X in AE.Die Planeten haben folgende (gerundete) Bahndaten, falls jemand nachrechnen möchte:
PlanetMittl. Abstand(AE)Siderische Umlaufzeit (Tage)Merkur0,3888Venus 0,72224,7Erde1,0365,25Mars1,52687Jupiter5,24 333Saturn9,510 759Uranus19,130 687Neptun30,0560 164Pluto39,590 700
Willy Mahl 16.10.2001
Letzte Änderung am 2009-Mar-15

Hinterlasse einen Kommentar
An der Diskussion beteiligen?Hinterlasse uns deinen Kommentar!