Die Helligkeit von Himmelsobjekten
Wenn man in den Nachthimmel schaut, so ist eines der auffälligsten Merkmale die verschiedene Helligkeit der sichtbaren Objekte. Es überrascht daher nicht, dass bereits Hipparch vor mehr als 2000 Jahren diese Situation zu ordnen und zu beschreiben begann. Er teilte alle sichtbaren Sterne in 6 Klassen ein. Die 20 hellsten fasste er zur 1. Klasse zusammen, in die 6. Klasse fielen alle Sterne, die man mit gutem Auge in mondloser Nacht gerade noch erkennen konnte. Diese nicht sehr objektive Methode wurde dann im 19. Jahrhundert durch quantitative Messungen erheblich verbessert.
Man hat herausgefunden, dass die hellsten Sterne am Himmel ca. 100 mal heller waren als diejenigen der 6. Klasse. Wenn man nun die Helligkeit in gleich große Klassen einteilt, so ergibt sich unter diesen Voraussetzungen ein Stufensprung von ca. 5. Wurzel aus 100 = 2,512.
Unter ungefährer Beibehaltung der Hipparchschen Einteilung definierte man dann: ein Stern 1. Größe ist exakt 100 mal heller als ein Stern 6. Größe.
Damit entspricht ein Unterschied einer Größenklasse einem Faktor von 5. Wurzel aus 100. Physiologisch macht die Einteilung in Größenklassen auch Sinn, denn das menschliche Auge empfindet die Helligkeit logarithmisch. Mit dem obigen Stufensprung ist die Helligkeitszunahme pro Größenklasse 2.512. Eine 100 fache Helligkeit wird vom Auge nur als fünfmal heller empfunden.
Jetzt hatte man einen objektiven Maßstab um die Helligkeiten zu beschreiben. Früher hat man Pollux und Formalhaut z.B. mit der Helligkeit der 1. Klasse beschrieben, jetzt war es möglich die Helligkeiten präzise für Pollux mit m = 1,16, und Formalhaut mit m = 1,19 zu beschreiben.
Mit m = Magnitudo hat man den Begriff der Größenklasse übernommen.
Die genauen Messungen der Helligkeiten haben zu einem allgemeinen Ansatz, dem Weber-Fechnerschen Gesetz geführt:
m1 – m2 = const * lg( H1 / H2 )
Für H1 / H2 = 100 wird m1 – m2 = -5 definiert und es ergibt sich dann die Beziehung : -5 = const * lg 100. Die Proprtionalitätskonstante ergibt sich so zu const = -2,5.
Somit ergab sich für die genaue Berechnung der Helligkeit die Beziehung:
m1 – m2 = -2,5 * lg( H1 / H2 )
Dass die Konstante negativ wird kommt daher, dass die zahlenmässig größere Klasse einer geringeren Helligkeit entspricht. Diese Beziehung findet immer dann Anwendung, wenn man die Größenklassen m und die entsprechende Helligkeit bzw. Lichtstärke ermitteln will. Mit dieser objektiven Beschreibung der Helligkeit, kann man jetzt beliebig starke oder schwache Helligkeiten beschreiben und die Klassen so nach oben und unten fortschreiben.
Was nun nur noch fehlt, ist eine Bezugshelligkeit eines bestimmten Sternes, zur Eichung des Systems. Zuerst wählte man dazu den Polarstern aus, stellte aber fest, dass seine Helligkeit nicht konstant ist und der Polarstern damit keinen absoluten Bezugspunkt darstellt. Heute ist die Skala durch die sogenannte Internationale Polsequenz festgelegt, mehrere Sterne in der Nähe des Himmelsnordpoles, deren Helligkeiten man fotoelektrisch sehr genau bestimmt hat. So folgt für die Helligkeiten anderer Himmelskörper:
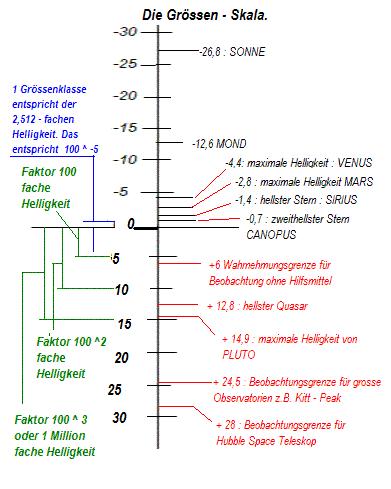
mSonne= -26,7; mMond= -12,7; mVenus= -3,9…-4,7; usw…
Nach dieser logarithmischen Skala ist eine Helligkeit von m = 24 z.B. um 18 Größenklassen lichtschwächer als die 6. Größenklasse, und entspricht einem Verhältnis der Helligkeiten von 1 : 16 Mio.
So ist
| Größenklasse | Helligkeitsunterschied zur Klasse |
| 0 | 12,5 |
| 1 | 2 |
| 2 | 6,610 |
| 3 | 15,85 |
| 4 | 39,81 |
| 5 | 100 |
| 6 | 251,2 |
| … | … |
| 15 | > 1 Mio. |
Größenklasse Helligkeitsunterschied zu Klasse 0 12,5 1 2 2 6,610 3 15,85 4 39,81 5 100 6 251,2… 15>1 Mio
Jetzt sind wir in der Lage folgende Frage zu beantworten: Wieviel Sterne der Größenklasse 6 leuchten so hell wie ein Stern mit m = 0?
Ja, es sind 251, wie aus der Tabelle hervorgeht. Durch Einsetzen von m1 = 0 und m2 = 6 und H1 = n * H2 in obige Formel bekommt man auch für n = 251.
 Die Lichtempfindung die ein Objekt im Auge des Beobachters hervorruft bezeichnet man als die scheinbare Helligkeit. Diese scheinbare Helligkeit sagt nichts über die wirkliche Helligkeit eines Objekts aus, da sich die Helligkeit mit der Entfernung eines Objekts ändert.
Die Lichtempfindung die ein Objekt im Auge des Beobachters hervorruft bezeichnet man als die scheinbare Helligkeit. Diese scheinbare Helligkeit sagt nichts über die wirkliche Helligkeit eines Objekts aus, da sich die Helligkeit mit der Entfernung eines Objekts ändert.
Wenn man die tatsächlichen Helligkeiten von Sternen vergleichen will, also die Strahlungsmenge die von einem Objekt in den Weltraum abgestrahlt wird, dann muss man den Einfluss der Entfernung eliminieren. Es wurde daher eine Normentfernung von 10 pc = 32,6 Lichtjahren festgelegt (1 pc = 1 Parsec, die Entfernung, in der der Radius der Erdbahn um die Sonne unter einem Winkel von einer Bogensekunde erscheint).
Diese Helligkeit in der Normentfernung von 10 Parsec nennt man “absolute Helligkeit” und bezeichnet sie mit “M”.
Wenn also die Entfernung eines Objekts bekannt ist, so kann man mit dieser Festlegung aus seiner scheinbaren Helligkeit die absolute Helligkeit M ermitteln. Die absolute Helligkeit eines Objekts ist die scheinbare Helligkeit die er in 10 pc Entfernung hätte. Diese Regelung erlaubt also einen Vergleich der absoluten Helligkeit der Objekte, weil die variable Distanz ausgeschaltet ist.
Die Lichtstärke ist umgekehrt proportional zum Quadrat der Entfernung. Daher gilt für das Verhältnis der Lichtstärken (L), welche dieselbe Lichtquelle in den Entfernungen d und 10 pc hervorruft:
L(d) / L(10 pc) = (10 pc / d) 2 oder mit Weber Fechner: m – M = 5 * lg(d / 10 pc) oder: 0,2 ( m – M + 5 ) = lg d nach M aufgelöst: M = m – 5 lg( d / 10), d in der Einheit Parsec nach d aufgelöst: d = 10 pc * 10(m – M) / 5 oder: d (pc)= 100,2 (m – M + 5). Diese Beziehung nennt man auch den Entfernungsmodul.
Dazu folgende Beispiele:
- Welche absolute Helligkeit (M) hat unsere Sonne, wenn ihre scheinbare Helligkeit m= -27 ist? Der Abstand des Beobachters ist d = 1,496 * 1011 m, dann wird M = +4,6.
- Ein Stern der Spektralklasse G2 wird mit m = +8 beobachtet, wie groß ist seine Entfernung? Aus dem HR – Diagramm ergibt sich M = +5. Daraus: d = 10 pc * 10(8 – 5) / 5 = 39,81 pc oder 39,81 * 3,26 Lichtjahre.
Die Leuchtkraft von Sternen
Welche Leuchtkraft hat ein Stern mit der absoluten Helligkeit von M = 0?
Als Ausgangsbasis nimmt man hier die Sonne, deren absolute Helligkeit MS = 4,62 ist und deren Leuchtkraft mit LS = 3,8*1026 W bekannt ist.
Da die absoluten Helligkeiten der Sterne auf dieselben Entfernungen bezogen sind, ist das Verhältnis der aus ihnen ermittelten Beleuchtungsstärken gleich dem Verhältnis der Leuchtkräfte.
M1 – M2 = -2,5 * lg( L1 / L2 ), oder: L1 = L2 * 10 0,4 ( M2 – M1 )
Für einen Stern mit der absoluten Helligkeit M=0 ergibt sich somit eine Leuchtkraft von L = 2,68 * 1028 W = 71 * LS.
Die Beziehung der absoluten Helligkeit M mit der Leuchtkraft L ergibt sich dann zu: M = -2,5 * lg ( L / 2,68 * 1028 W )
Nun hat man ein Instrument um die von den Sternen abgestrahlte Energiemengen zu vergleichen.
Jetzt ist man in der Lage zu ermitteln, dass Sirius z.B. 23 mal mehr Energie abstrahlt als die Sonne, und somit 23 fache Leuchtkraft der Sonne besitzt. Ferner, dass Rigel im Orion über die 1000 fache Leuchtkraft des Sirius verfügt und 23 000-fache Leuchtkraft der Sonne hat.
Über die Masse – Leuchtkraftbeziehung kann man dann auch noch die Masse der Sterne bestimmen. Wenn man den Radius eines Sterns bestimmen kann (z.B. über ein Interferometer) so kann man aus M, und dem Radius, auch noch die Temperatur an der Oberfläche des Sterns ermitteln.
Willy Mahl 05.07.2000
Letzte Änderung am 2009-Mar-15

Hinterlasse einen Kommentar
An der Diskussion beteiligen?Hinterlasse uns deinen Kommentar!