STERNE
O – B – A – F – G – K – M
… das ist das Alphabet der stellaren Astronomie, die Sequenz der Spektraltypen, die Grundlage unseres Wissens über die Sterne. Das Verständnis des Spektrums erschließt uns die physikalische Natur der Sterne. Wie unsere Sonne, sind alle Sterne riesige Nuklear-Öfen, die Masse in Energie umwandeln (E = m * c2). Als Nebenprodukt versorgt unsere Sonne die Erde mit Licht und Wärme und ermöglicht damit unsere Existenz.
Der nächste Stern, die Sonne, ist ein echter Durchschnittsstern und damit typisch in jeder Beziehung. Ihr Licht entsteht durch Kernfusion, wie bei einer bemerkenswert gut kontrollierten Wasserstoffbombe. Obwohl Sterne einen unveränderlichen, konstanten Eindruck erwecken, unterliegen sie einer steten Veränderung, während ihre Masse als Brennstoff verbraucht wird. Die Sonne hat eine Lebensdauer von ca. 10 Milliarden Jahren und ist derzeit in einer stabilen Phase ihres langen Lebens.
Die wichtigste physikalische Größe eines Sterns ist seine Masse. Sie bestimmt den Lebenslauf des Sterns und seine Lebensdauer. Im Vergleich zu anderen Sternen liegt die Sonne ungefähr in der Mitte einer Verteilung, die bei ca. 1/10 der Sonnenmasse beginnt, und bei der 100-fachen endet. Die Charakteristik und das Schema der Sternevolution wird mit dem Werkzeug der Spektralklassen untersucht, und im sogenannten Hertzsprung-Russel-Diagramm (HRD) dargestellt:
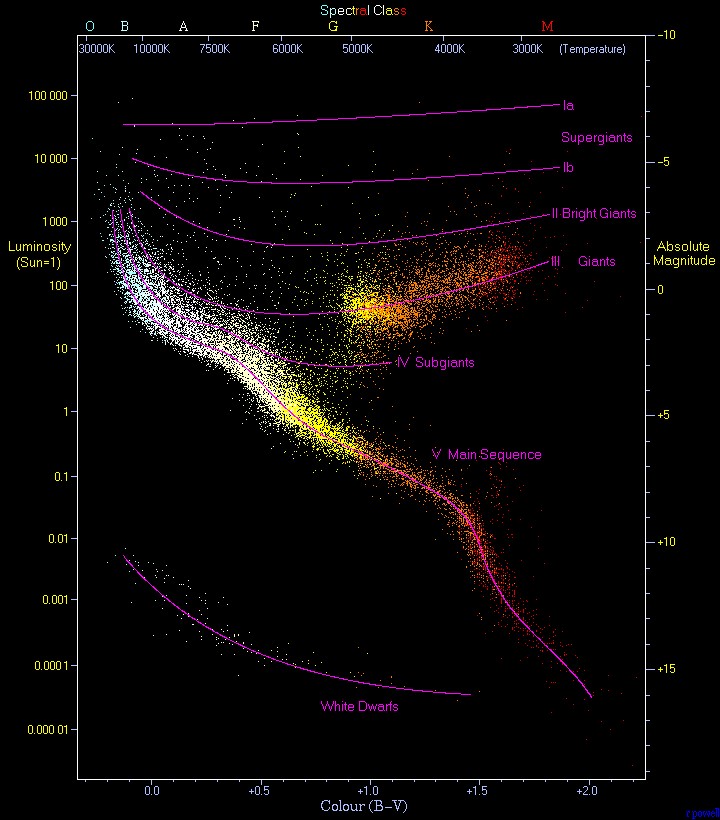
Im Hertzsprung-Russell-Diagramm liegen die meisten Sterne auf der Hauptreihe (Main Sequence), sie haben Temperaturen im Bereich zwischen ca. 3 000 K und ca. 30 000 K.
In einer groben Vereinfachung besteht das Universum nur aus Wasserstoff und Helium, den einfachsten Elementen, die am Anfang vor ca. 14 Milliarden Jahren entstanden sind. Der Kern der Sterne produziert die schwereren Elemente, die wir auf der Erde und auf den anderen Planeten antreffen. Die äußeren Schichten der Sterne in unserer Umgebung folgen jedoch der generellen Regel 90% H, 10% He, und nur 0,1% aller anderen Elemente (% nach Teilchenanzahl).
Im Gegensatz dazu sehen wir, dass unsere Erde von schweren Elementen dominiert wird und damit eine Sonderstellung einnimmt. Alle Planeten des Sonnensystems sind Gebilde, in denen sich die schweren Elemente konzentriert haben. Gewöhnlich dominiert Sauerstoff die Gruppe der schwereren Elemente, gefolgt von Kohlenstoff und Stickstoff.
Sterne entstehen häufig in Gruppen, Doppel- und Mehrfachkombinationen. Doppelsterne gibt es mehr als einzelne Exemplare, und sie sind äußerst nützlich, um die Masse von Sternen zu bestimmen.
Wenn die Umlaufperiode T und die mittlere Entfernung a der beiden Sterne voneinander bekannt sind, können wir ihre Masse berechnen. Das 3. Keplergesetz und Newtons Gravitationsgesetz zeigen den Zusammenhang von T, a und der Summe der Massen M1 und M2 der beiden Sterne:
G (M1 + M2) = 4 * π2 * a3 / T2
Dabei ist G die Gravitationskonstante, T und a gewinnt man durch Beobachtung.
Wenn man durch sorgfältige Beobachtung auch das Zentrum des Massensystems der beiden Massen bestimmen kann, so ist sogar eine Bestimmung der Einzelmassen möglich. Die Distanz der Körper ist reziprok zum Verhältnis der Massen (wie beim Hebelgesetz).
Als Beispiel sei das Verhältnis der Abstände von Erde und Mond vom gemeinsamen Massenzentrum genannt. Das Massenzentrum ist 80 mal näher bei der Erde als beim Mond, da die Erde die 80-fache Mondmasse hat. Daher ist der Erdorbit 1/ 80 der Distanz zum Mond, oder 5000 km vom Erdzentrum entfernt, also immer noch ca. 2000 km unter der Erdoberfläche.
Die Hauptreihe des HRD repräsentiert eine kontinuierliche Massensequenz der Sterne. Die größten Sterne entsprechen ca. 100 Sonnenmassen oder mehr, die kleinsten nicht mehr als 1/10 der Sonnenmasse.
Sterne formieren sich in Gruppen. Unsere Sonne war auch Teil eines Sternhaufens, der sich später aufgelöst hat. Genau genommen befindet sie sich immer noch innerhalb eines sehr dünnen offenen Haufens, bestehend aus den mittleren 5 Sternen des großen Wagens, Sirius , Alpha Coronae Borealis, und einigen anderen.
Obwohl man von Fixsternen spricht bewegen sich die Sterne im Raum meist mit sehr hohen Geschwindigkeiten. Ihre Entfernung zur Erde ist jedoch so groß, dass man diese Bewegung innerhalb eines Menschenlebens nicht wahrnimmt.
Das elektromagnetische Spektrum und das Sternenlicht sind neben den geometrischen und anderen physikalischen Größen wichtige Eigenheiten von Sternen.
Die Lichtgeschwindigkeit ist c = Wellenlänge * Frequenz. Elektromagnetische Wellen transportieren Energie. Die Energie eines Photons ist direkt proportional zu seiner Frequenz f, bzw. umgekehrt proportional zu seiner Wellenlänge λ:
E = h * f = h * c / λ ;
dabei ist h = 6,6 * 10-27 erg*s die Planck-Konstante.
Beispiel: Bei der Frequenz von f = 5,5*1014 Hertz (grünes Licht) ergibt sich eine Photonenenergie von 3,6*10-12 erg.
Zum Vergleich: eine Strahlungsleistung von 1 W = 107 erg/s. Eine Standard 100 W Birne emittiert also ca. 1020 Photonen pro Sekunde.
Das elektromagnetische Spektrum überträgt nicht nur Energie, sondern auch Information über die Quellen der Strahlung.
Verschiedene Arten von Information über Temperaturen, Dichte, Zusammensetzung und Bewegung kommen über verschiedene Wellenlängen an. Das meiste was wir über Sterne wissen ist im optischen Spektrum zu finden. Daten über die galaktische Rotation zum Beispiel, bekommt man aber aus Radiobeobachtungen. Das Wissen über Hochenergieprozesse in Galaxien kommt von Röntgen-Strahlen.
Die Astronomie beobachtet das gesamte Spektrum. Unsere Atmosphäre ist hierbei jedoch ein Hindernis, daher werden nicht nur opische Teleskope, sondern auch andere Messgeräte über die Atmosphäre ins Weltall geschossen.
Die Helligkeit von Sternen
Die scheinbare Helligkeit m eines Sterns, wie sie von dem Beobachter auf der Erde gemessen wird, entspricht einem Strahlungsstrom in W/m2 (Watt pro Quadratmeter).
Da die Astronomie eine sehr alte Wissenschaft ist, hat man von den alten Griechen ihre Maßstäbe der Einteilung in Helligkeitskategorien im Prinzip übernommen. Sie haben die Sterne nach ihrer Helligkeit in „Größenklassen“ eingeteilt, auch Magnituden (mag) genannt.
1 mag waren die hellsten Objekte und 6 mag die gerade noch mit bloßem Auge wahrnehmbaren. Dieses System entspricht einer logarithmischen Helligkeitsskala. Die Differenz von 5 Magnituden entspricht dabei etwa einem Faktor von 100 beim Strahlungsstrom. Daraus resultiert die Festlegung:
1 Magnitude Differenz entspricht dem Faktor 1001/5 = 2,512 beim Strahlungsstrom. [F01]
Beispiel: Ein Stern mit 3 mag hat einen 2,512 fach höheren Strahlungsstrom als ein Stern mit 4 mag.
Die Skala ist so definiert, dass hellere Sterne einer kleineren Größenklassen zugeordnet werden. Dadurch bekommen besonders helle Objekte auch Werte, die kleiner als 1 mag sind oder sogar negativ sind.
Zum Beispiel:
| Objekt | Größenklasse |
| Sonne | -27 mag |
| Vollmond | -12 mag |
| Venus | -4,7 mag (in ihrem hellsten Glanz) |
| Jupiter | -2,9 mag (in seinem hellsten Glanz) |
| Sirius | -1,46 mag |
| Wega | ~0 mag |
| Arktur | -0,4 mag |
Mit optischen Hilfsmitteln erreicht man eine Erweiterung des Sichtbarkeitsbereiches des menschlichen Auges auf erheblich höhere Werte:
| Gerät | Grenzgröße (ca.) |
| Fernglas | 8 mag |
| Kleines Teleskop | 11,5 mag |
| Teleskop vom Mount Palomar | 26 mag |
| Weltraum-Teleskope | 30 mag |
Das Mount Palomar Teleskop kann also 20 mag schwächere Objekte am Himmel wahrnehmen als das menschliche Auge. Das entspricht einem 100(20*1/5) = 100 000 000 fach kleineren Strahlungsstrom. Die scheinbare Helligkeit kann mit einem photoelektrischen Gerät gemessen werden, das im Fokus eines Teleskops den Strahlungsstrom in elektrischen Strom umwandelt.
Die absolute Helligkeit
Die auf der Erde wahrnehmbare Helligkeit eines Sterns hängt von 2 Variablen ab: seiner wahren Leuchtkraft (Betrag der Energie, die der Stern pro Zeiteinheit abstrahlt) und seiner Distanz vom Beobachter. Um die wahren Helligkeiten der Sterne zu vergleichen, muss man die unterschiedlichen Distanzen berücksichtigen.
Das hierbei verwendete Gesetz besagt, dass die ankommende Strahlungsleistung (Leistung = Energie pro Zeiteinheit) umgekehrt proportional zum Quadrat des Abstandes von der Strahlungsquelle ist, also P~1/d2 (P= Strahlungsleistung, d = Distanz).
Um nun eine Bezugsbasis für den Vergleich der Helligkeiten verschiedener Objekte zu schaffen, hat man eine Standardentfernung von 10 pc (Parsec) gewählt. (1 Parsec = 3,26 Lichtjahre). Bei dieser Entfernung werden die Helligkeiten miteinander verglichen. Die Helligkeit, die ein Objekt in 10 pc Entfernung haben würde, nennt man seine absolute Helligkeit M. Sie ist ein Maß für die wahre Leuchtkraft des Objektes.
Die Beziehung: M = m + 5 – 5*log d, bzw. umgeformt: log d = 0,2 ( m – M + 5 ) zeigt den Zusammenhang zwischen der absoluten Helligkeit M, der scheinbaren Helligkeit m und der Distanz d in pc. Der Wert m – M wird auch Entfernungsmodul genannt.
Farben der Sterne und ihre Temperatur
Selbst ein kurzer Blick zum Sternenhimmel zeigt uns die verschiedenen Farben der Sterne. Diese Farben haben eine enge Beziehung zum Spektraltyp und der Oberflächentemperatur. Das Sternenlicht, das wir empfangen, ist immer ein Mix aller Farben. Das Auge ist ein eher gelb empfindlicher Detektor. Daher sehen wir von mehreren gleich hellen Sternen gelbe Sterne als die hellsten!
Farben erlauben uns, die Temperatur der Oberfläche eines Sterns zu bestimmen. Das Farbspektrum (Strahlungsleistung abhängig von der Wellenlänge) der meisten Sterne entspricht ungefähr dem eines „Schwarzen Strahlers“. Die Wellenlänge der maximalen Emission ist umgekehrt proportional zur Temperatur:
Lmax = 2,9 * 107 / T
Dabei ist Lmax die Wellenlänge der max. Emission in Ångström (Å), T die Temperatur in Kelvin (K).
Diesen Zusammenhang nennt man das Wiensche Verschiebungsgesetz.
Die totale produzierte Leistung pro Flächeneinheit beschreibt das Stefan-Boltzmann-Gesetz:
P ~ Sigma * T4 (Sigma ist die Stefan-Boltzmann-Konstante)
Multipliziert mit der Oberfläche des Sterns ( 4*π*R2) ergibt sich für die gesamte abgestrahlte Leistung (Leuchtkraft):
Pges = 4*π*R2 * Sigma * T4 . [F02]
Die Temperatur eines Sterns kann man also bestimmen, indem man P und R misst und die Gleichung nach T auflöst. Man nennt T die effektive Temperatur. Die Sonne hat z.B. eine effektive Oberflächentemperatur von 5 770 K.
Wie groß sind Sterne?
Wenn man mit Formel [F02] die Werte von P, R und T ins Verhältnis zu den entsprechenden Werten der Sonne setzt, ergibt sich
PStern / PSonne = (RStern / RSonne)2 * (TStern / TSonne)4 . [F03]
Damit kann man aus Leuchtkraft und Temperatur eines Sterns seinen Radius in Sonneneinheiten ermitteln.
Beispiel:
Einer der hellsten Super-Riesen am Himmel ist der „Granatstern“ Mü Cephei (μ Cep) mit einer absoluten (bolometrischen) Helligkeit von MStern= -8,5 Mag, unsere Sonne hat MSonne = 4,74. Diese Helligkeitsdifferenz von MSonne – MStern = 13,24 Magnituden bedeutet nach Formel [F01], dass μ Cep um den Faktor 2,51213,24 ≈ 200 000 mal leuchtkräftiger ist als unsere Sonne, also PStern / PSonne = 200 000. Die effektive Temperatur von μ Cep ist ca. 3750 K, die der Sonne 5770 K.
Mit diesen Werten ergibt [F03] einen Radius von μ Cep, der 1060 mal größer ist als der der Sonne. Dies entspricht 740 Mio. km, also etwa der Größe der Jupiterbahn!
Ein direkter Weg, Sternradien zu finden, ist die Ermittlung von Distanz und Winkeldurchmesser des Sterns.
Der Mond ermöglicht dazu eine sehr effiziente Methode. Er bewegt sich mit 0,55″ (Bogensekunden) pro Zeitsekunde gegen den stellaren Hintergrund und bedeckt somit Sterne. Man kann die Zeit messen, in welcher der Stern hinter dem Mond verschwindet. Mit dieser Methode kann man jeden Stern innerhalb von 5° Abweichung von der Ekliptik, innerhalb einer 18-jährigen Periode vermessen.
Eine andere Methode ist die Bestimmung des Winkeldurchmessers mittels eines sogenannten Speckle-Interferometers.
Die Struktur der Sterne
Ein Stern wird in 3 Zonen aufgeteilt, diese sind Kern, Hülle und Atmosphäre.
Im Kern eines Sterns wird Energie durch thermonukleare Fusion nach E = m * c2 produziert. Die Temperatur, um den thermonuklearen Prozess auszulösen, muss mindestens 5 Mio. K hoch sein. Nur ein Bruchteil des Kerns hat diese Temperatur.
Die Hülle beinhaltet fast den Rest der Masse des Sterns. Die Last der Hülle drückt das Innere des Sterns zusammen, ähnlich dem Kolben eines Dieselmotors in der Kompressionsphase, bis es zur Selbstzündung kommt. Die Hülle bildet aber auch eine Isolierschicht, die die Energie, die im Innern produziert wird, nicht zu schnell nach außen dringen lässt. Bei 107 K im Kern der Sonne z.B. benötigt die Strahlung, bis sie bei uns ankommt, ca. 100 000 Jahre!
Die Atmosphäre hat im Vergleich eine sehr geringe Masse. Sie ist jedoch die Schicht, in der das Emissions-Spektrum produziert wird, das wir auf der Erde messen.
Evolution der Sterne
Der größte Teil der Sterne sind Wasserstoffbrenner und liegen daher auf der Hauptreihe des HRD, entsprechend ihren Massen. Eine größere Masse hat einen größeren Kern zur Folge und daher mehr „Treibstoff“, aber auch einen größeren Verbrauch. Die innere Temperatur steigt. Die Rate der thermonuklearen Reaktion ist außerordentlich empfindlich auf diesen Parameter, mit dem Ergebnis, dass Sterne größerer Masse sehr viel höhere Leuchtkraft haben als Sterne geringer Masse.
Ein Stern mit 10-facher Masse der Sonne ist 10 000 mal heller als diese. Je massenreicher die Sterne sind, desto schneller verbrauchen sie ihre Brennstoffvorräte, so dass sie trotz höherer Vorräte eine erheblich kürzere Lebensdauer haben. Wenn dann der thermonukleare Ofen im Kern erloschen ist, kontrahiert der Stern unter seinem Gravitationsdruck. Die Temperatur im Inneren steigt an und initiiert eine weitere Fusion am inneren Rand der Hülle, bei der Helium unter Abgabe von Energie in Kohlenstoff verwandelt wird. Der Stern wird wieder heller, die äußere Hülle bläht sich auf und wird so groß, dass trotz höherer Gesamthelligkeit die Sternatmosphäre abkühlt. Der Stern ist nun ein Riese geworden und von dem Hauptast des HRD abgewandert. Sternwinde aus der aufgeblähten Hülle führen zu einem erheblichen Massenverlust. Nach weiteren Transformationen endet der Stern schließlich als weißer Zwerg, nahezu die gesamte Hülle wurde in den Weltraum abgestoßen. Dies ist die Entwicklung von Sternen in der Kategorie unserer Sonne.
Sterne mit sehr großen Massen verhalten sich anders. Wenn ihr Brennstoff verbraucht ist, blähen sie sich zu Super-Riesen auf, sie werden im Kern sehr heiß, so dass sogar schwere Elemente bis zum Eisen entstehen können. Dann explodieren sie als Supernova. In diesem Prozess werden dann die Elemente schwerer als Eisen kreiert.
(Erst nach 1950 fand man, dass die meisten der chemischen Elemente in Sternen produziert werden. Nur die leichtesten H und He rühren vom Urknall her. Unsere Sonne wird sich in einigen Milliarden Jahren zu einem roten Riesen aufblähen, bevor sie im Endstadium zu einem weißen Zwerg zusammenschrumpft. Die verschiedenen Entwicklungsphasen werden durch unterschiedliche Reaktionen im Inneren der Sterne geprägt. Die Umwandlung von C in N z.B. kann nur in heißen Himmelskörpern erfolgen. In Sternen werden alle Elemente bis zum Eisen produziert. Die schwereren Elemente entstehen hauptsächlich beim Kollaps der Sterne, also in einer Supernova.)
Die Kompression durch den Gravitationsdruck in Sternen ist die Ursache für die hohe Kerntemperatur, die den nuklearen Zündpunkt überschreitet. Sterne mit größeren Massen haben demzufolge eine höhere Temperatur, einen größeren Kern und damit mehr Brennstoff zur Verfügung. Der vorhandene Brennstoff produziert Energie in einem viel höheren Maße pro Masseneinheit. Als Konsequenz des Gravitationsdruckes von Sternen mit großen Massen, leuchten die Sterne mit einer viel größeren Helligkeit als kleinere Sterne. Für Sterne auf der Hauptreihe des HRD mit Masse M gilt: L ~ M3,5 . (L Leuchtkraft, M Masse).
Die stellare Lebensdauer hängt vom Betrag der Masse ab, die verbraucht wird, dividiert durch die Verbrauchsrate. Der Verbrauch ist viel höher bei Sternen großer Massen, so dass die höheren Reserven an Brennstoff sogar zu einer kürzeren Lebensdauer führen, und zwar zu einer dramatisch kürzeren.
Die ungefähre Lebensdauer t eines Sterns ist proportional zu M / Brennrate.
Die Brennrate ist proportional zur Helligkeit L, es ist also: t ~ M / L; L ist proportional zu M3,5, also ist t ~ M / M3,5 = 1 / M2,5 .
Unser Wissen von der Sonnenstruktur ergibt eine Lebensdauer der Sonne von tSonne = 1010 Jahre. Ein Stern von der 10-fachen Sonnenmasse hat dann eine Lebensdauer von t = (1 / 102,5)*tSonne = (1 / 300)*tSonne, d.h. nur 33 Mio. Jahren.
Das andere Extrem: Für eine Sternmasse von 1/10 der Sonnenmasse, M = (1/10) * MSonne, ergibt sich t = (102,5) * tSonne , d.h. t = 300 * 1010 = 3 * 1012 = 3 Billionen Jahre.
Selbst wenn diese Formel etwas ungenau ist, so zeigt sie doch den grundsätzlichen Zusammenhang sehr deutlich.
Die Geburt von Sternen
Aus dem Chaos einer interstellaren Wolke findet die erste Kontraktionsphase eines Sterns statt. Die Entwicklung wird bestimmt durch Gravitationskräfte und magnetische Kräfte in magnetischen Feldern, die in der Wolke wirken. Der Prozess ist komplex und noch nicht völlig verstanden. Sicher ist, dass der Prozess dem allgemeinen physikalischen Gesetz der Erhaltung des Drehimpulses folgen muss.
l = m * r × v
Dabei ist m = Masse; v = Bahngeschwindigkeit; r = Bahnradius; l = Drehimpuls.
Der gesamte Drehimpuls aller Bestandteile eines geschlossenen Systems ist konstant.
Interstellare Wolken drehen sich nicht schnell, aber sie sind riesengroß und beinhalten daher einen Riesendrehimpuls. Wenn die Wolke infolge ihrer Gravitation kontrahiert, muss die Geschwindigkeit ansteigen. Man kann sich leicht vorstellen, dass der Stern vor seiner Entstehung in Stücke gerissen würde, wenn er seinen Drehimpuls nicht los werden könnte. Wie das funktionieren kann, ist ein aktuelles Thema der Forschung.
Willy Mahl 17.02.02
Überarbeitet 2024-06-14, ek

Tja, was soll man zu diesem sicher gut gemeinten, aber leider misslungenen Beitragsversuch sagen ?
Offenbar ist die Darstellung von sehr großen oder kleinen Zahlen in der Exponentialschreibweise in Baden-Wurtemberg für manch einen eine intellektuelle Überforderung, was nicht nur an der Unfähigkeit liegen dürfte, einen Text sorgfältig zu formatieren, wozu auch das Höher- und Tieferstellen von Ziffern und Zahlen in der Exponentialschreibweise (oder in chemischen Formeln) zählt. Anders sind Teile des Beitrages wie etwa :
„Multipliziert mit der Frequenz von gelbem Licht z.B. 5,5*1014 Hertz, ergibt eine Energie von 3,6*10-12 erg.
Zum Vergleich: eine Strahlungsleistung von 1 W = 107 erg/s. Eine Standard 100 W Birne emittiert also 1020 Photonen pro Sekunde.“
Oder : „1m = 1001/5 = 2,512“
Oder auch : „t ~ M / M3,5 = 1 / M2,5″
nicht mehr nachvollziehbar.
Zu Ihrer Information : wenn man in einem Text einen Exponenten nicht hochzustellen vermag, dann macht man das alternativ durch Einfügung des Zeichens “ ^ “ zwischen Basis und Exponenten, auch negativen Exponenten.
Der Text MUSS also diesbezüglich völlig überarbeitet werden !
So ist 1 Magnitude mitnichten 1001/5 (= 200,2), sondern 100^ (1/5), also die fünfte Wurzel aus 100.
Und das ist tatsächlich 2,512.
Eine 100 W Glühbirne emittiert nicht 1020 Photonen pro Sekunde, sondern 10^20 Photonen, das sind überschaubare 100.000.000.000.000.000.000 Photonen pro Sekunde, 100 Quintillionen, und NICHT etwa 1.020.
Und t ist nicht proportional zu M/M3,5, sondern t ~ M/M^3,5 = 1/M^2,5 = M^-2,5.
Usw. Ihr Text wimmelt von Fehlern. Hätte mein damaliger Mathematiklehrer DIESEN BEITRAG gesehen, hätte den vermutlich der Schlag getroffen bezüglich der aus diesem Text erkennbaren Schwächen des Bildungsstandortes Deutschland.
Ich will ja eigentlich keinesfalls beleidigend sein, aber offenbar können (manche) Baden-Würtemberger auch noch andere Dinge nicht, neben Hochdeutsch.
Der Beitrag ist keinesfalls geeignet, interessierten jungen Menschen das Thema Astronomie näher zu bringen. Jedenfalls nicht so.
Und die im Ausland werden sich (völlig berechtigt !) fragen, was aus dem Land der „Dichter und Denker“ zwischenzeitlich geworden ist. Das kann nur noch besser werden !
Wir haben den Artikel berichtigt. danke für den freundlichen Hinweis.