Bestimmung der Mondentfernung durch Messung am Teleskop

Die in der Folge beschriebene Methode wurde von mir auf der Sternwarte entwickelt und ausgeführt. Gleich vorab: sie ist nicht genau und wird strengen Maßstäben nicht gerecht.

Der Hauptgrund dafür liegt darin, dass eine idealisierte Mondbahn zugrunde gelegt wird, die ja wie man weiß, nicht den Tatsachen entspricht, denn die Mondbahn ist ja die komplexeste des gesamten Sonnensystems. Nicht zu vermeidende Messfehler, werden also durch diese Prämisse noch verstärkt.

Die Methode

Trotzdem möchte ich diese Methode nicht zu den Akten legen, sondern hier erwähnen, da ich glaube, dass sie einen gewissen didaktischen Wert hat, und z.B. Schüler mit dem Prinzip der geometrischen Entfernungsmessung vertraut machen kann.

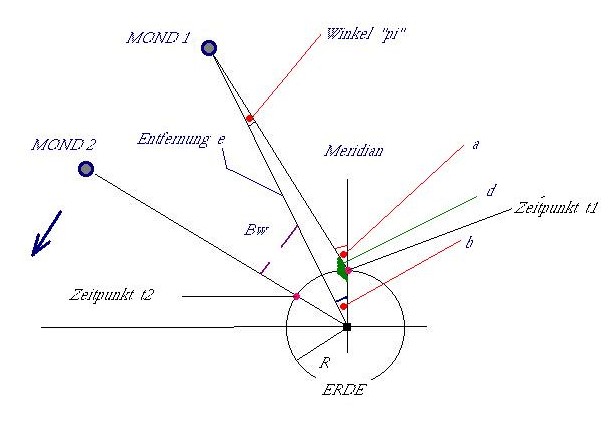
Die Messung sollte bei einer Monddeklination = 0° durchgeführt werden. Folgende Größen

t1 Zeitpunkt zu Beginn der Messung, möglichst früh nach dem Aufgang des Mondes 

t2 ist der Zeitpunkt wenn der Mond im Meridian steht 

a  ist der Winkel zwischen Mond und Meridian zum Zeitpunkt t1

Bw ist die Winkelbewegung des Mondes zwischen t1 und t2in Bogensekunden und errechnet sich aus der Eigenbewegung des Mondes: sid. Monat = 27d07h43m11,6s = 2 360 591,6s Bw = ( t2 – t1 ) * 0,549″/s (360° =1 296 000″, d.h. der Mond bewegt sich in 1s um 0,549″ auf seiner Bahn weiter).

Aus der Skizze ergibt sich für die Winkel:d = 180° – ac= (t2-t1) * 15,041°/h ist der Winkel zum Zeitpunkt t2 zwischen dem Meridian und dem Rektaszensionskreis, der zum Zeitpunkt t1 im Meridian stand. Oder anders und einfacher gesagt, der Winkel, um den die Erde während der Meßdauer weiter rotiert ist. b =  c  – Bw pi = 180° – ( b + d )

Daraus ergibt sich nach dem Sinussatz: sin pi / sin d = R / e oder nach Umformung e = R ( sin d / sin pi )

Messung vom 26.9.1996 auf der Sternwarte Höfingen

Zeitpunkt der Messung 19 h 30 MESZ ( Mondfinsternis ist am 27.9.96 um 4h54m)

Deklination des Mondes ca 1°

Stundenwinkel des Mondes zum Messbeginn 18h40m, daraus folgt a = 80,00°

Mit t2 – t1 = 5h28m32,2s =19 712s   folgt c = ( t2 – t1 ) * 15,041°/h = 82,36°

d = 180° – a = 100,00°

Bw = (t2-t1) * 0,549″/s = 19 712,2 sec * 0,549 = 10 822″ = 3,01°

b = c – Bw = 82,36° – 3,01° = 79,35°

pi = 180° – ( b + d ) = 180° – ( 100,00° + 79,35° ) = 0,65° = 39″

e = R / sin pi = 6 378 km / sin 0,65° = 562 000 km

Der wirkliche Mondabstand war andiesem Tag ( um 20h ) = 365 802 km geozentrisch.

Das Ergebnis ist mit 54 % Abweichung wahrlich nicht umwerfend, ich bin jedoch davon überzeugt, dass die Methode noch ein genaueres Ergebnis hergibt, wer will es versuchen?

Viel Spaß beim Ausprobieren.

Willy Mahl, 11.03.02

---

Letzte Änderung am 12.09.2002 durch astroman